In a traditional desktop application, the application holds its own data and that data is available whenever we need to present it to the user. In a web application, the data is stored on the web server and the client (typically a web browser) has no direct access to it. We say that it acts as a stateless client in relation to the web server. This means that for each logged on client, the server must store information about it. This information is known as a session. When the client logs on, a new session is created. To identify a session, we use unique session identifiers. Upon login, the client is informed about its session identifier, which is can supply in subsequent calls to the server. When a session is no longer needed, it is destroyed; either because the client makes an explicit logout call to the server, or because the server has detected that the session has not been used in a while.
The minimal information needed about a session is its ID, which the client provides when calling methods in the server, and the time when it was last accessed, which the server uses to know if it should destroy the session because it has been inactive for too long.
We will call the main interface, through which we access our sessions, the session manager. The following requirements must be met by our session manager:
- It must be able to create a new session on request.
- It must be able to give us an existing session, when we need it.
- It must be able to delete a session when we are done with it.
- It must automatically remove a session that has not been accessed for a certain time.
The operations must be reasonably efficient; we will use a hash table to store the sessions, which means that in most cases, we will be able to access a specific session in constant time. In addition to the hash table, we will use a double-linked list to be able to efficiently determine if a session has been inactive for too long and must be destroyed. We will start by focusing on the hash table, and return to the list a bit later.
The hash table
Note: this article was originally written for use with an older version of Delphi, which does not have the new collection classes. If I were to use Delphi 2009 or later, I would not implement my own hash table class, but use the TDictionary class instead. This section however will contain a short introduction to hash tables and describe a proposed implementation.
We will use the Cardinal type for our session IDs. Ideally, to store all our sessions in a way that lets us insert and access the elements in an efficient manner, we would like to use an array of 2^32 elements. This would require us to allocate 4 GB of memory to hold the array, which is not (yet) realistic.
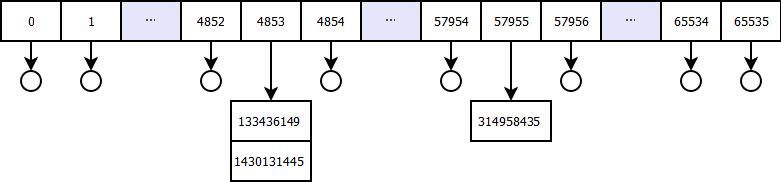
If we can create a function that uniquely maps a Cardinal value to a smaller value, we can create an array of say 2^16 elements, and store our sessions there. Such a function is called a hash function, and in this case, it will be an easy task to create it. We will simply look at the right-most 16 bits of a cardinal value, and insert our Cardinal value into the corresponding slot in our array. The following list shows the index (16-bit value) for a number of Cardinal numbers (32-bit value). The correspondence between the Cardinal value and the array index is easier to see when regarding the hexadecimal representation of the values:
| Value | Index |
|---|---|
| 1430131445 ($553E12F5) | 4853 ($12F5) |
| 133436149 ($07F412F5) | 4853 ($12F5) |
| 314958435 ($12C5E263) | 57955 ($E263) |
As we can see, more than one Cardinal value may map to the same index in the array. Thus, we will place a pointer to a TList object in each array element, and place our actual objects in that list. The following picture shows the situation after the values above have been inserted:
Most array items contain a nil pointer, but for items 4853 and 57955, we have created TList objects into which we have inserted 1 and 2 items respectively. In reality, we will not insert only the Cardinal values, but session objects (of the TSessionContainer type described below) that among other things contain the ID.
Ideally, we would like an array that can hold as many elements as we may have sessions, i.e. 2^32 elements, which will give us immediate access to any object. As stated above, this is not possible, so we have to use fewer elements, and place more than one object in each element. Initially, elements in the array will hold either zero or one object, which will give us the fast access we want. As the total number of objects grows however, more and more elements will hold more than one object. If we use all 2^32 possible session IDs, each of the 65536 array elements will point to a list, which in turn holds 65536 objects. To find a particular object, we will find the correct array index quickly, but then traverse up to 65536 list items before we find the correct object. With this many sessions, a binary search tree would give us faster access to individual objects.
One of the test projects in the code accompanying this post tests the performance of our list when we use a different number of objects. In the tables below, you can see how many elements in the array, on average, that point to lists with one, two, three etc. objects.
| 10000 sessions | 1st run | 2nd run | 3rd run | 4th run | 5th run | Avg. |
|---|---|---|---|---|---|---|
| Elements pointing to 1 object | 8652 | 9982 | 7878 | 7425 | 9212 | 8629,8 |
| Elements pointing to 2 objects | 674 | 9 | 1061 | 1193 | 394 | 666,2 |
| Elements pointing to 3 objects | 0 | 0 | 0 | 63 | 0 | 12,6 |
With 10000 sessions, locating a specific session requires traversing approximately 1,1 items in a list.
| 20000 sessions | 1st run | 2nd run | 3rd run | 4th run | 5th run | Avg. |
|---|---|---|---|---|---|---|
| Elements pointing to 1 object | 12940 | 13538 | 14815 | 14002 | 13126 | 13684,2 |
| Elements pointing to 2 objects | 3530 | 864 | 2252 | 2108 | 3434 | 2437,6 |
| Elements pointing to 3 objects | 632 | 227 | 594 | 2 | 291 | |
| Elements pointing to 4 objects | 417 | 83,4 | ||||
| Elements pointing to 5 objects | 234 | 46,8 |
With 20000 sessions, locating a specific session requires traversing approximately 1,2 items in a list.
I will not bore you with tables describing the number of objects per element for higher number of sessions, but for 100000 sessions, locating a specific session requires traversing approximately 2 items in a list. For 500000 sessions, the number is approximately 5 items, and for 1000000 sessions, approximately 8. Since there are only 65536 lists to choose between, it is easy to see that as the number of sessions increase, so will the average number of items per list.
The linked list
A linked list is a “chain” of objects, where each object, in addition to some data, holds a pointer to the next object in the list. In a double-linked list (as opposed to a single-linked list), each object also holds a pointer to the previous object in the list.
In a double-linked list, inserting or removing an element at either end of the list is a constant operation, since we only need to manage one or two pointers, regardless of how many objects the list holds. Also, when we have an object, removing it from the list is a constant operation (in this case, we only have to change up to four pointers, regardless of the list’s size). Locating an object in the list however, is proportional to the number of items in the list, since we have to traverse the list, item by item, until we find what we are looking for. Thus, if you need to locate an element, a linked list is probably not a good choice. In the session management structure, this will not be a problem since we will first locate the session objects using the hash table described above. In the implementation of our list, which we will refer to as the time list, we will keep the items sorted by the session’s access time, and I have therefore decided to name the pointers “Older” and “Newer” instead of the more familiar “Next” and “Previous”, to make the code easier to read.
A note of caution: do not confuse a linked list with Delphi’s TList class, which is implemented using an array as the underlying structure.
Implementation
We will have a base class for sessions, which is derived from TObject. When you implement a system that needs session management, you will derive your own session class from this. We will not add any functionality in the TSession class, but to make the actual session creation work we must introduce a virtual constructor at this level.
TSession = class public constructor Create; virtual; end;
One aspect of the linked list structure is that, unlike for e.g. an array, there is no “container structure” that holds all the nodes – each node has pointers to the nodes immediately before and after it in the list, and all we need to access the list is a pointer to the first or the last node (in our case, we will maintain pointers to them both).
What we need is a structure that can act as a container for a session object, containing the session ID and maintain the pointers we need for the linked list. We will call this object a session container:
TSessionContainer = class protected ID: Cardinal; Session: TSession; Older: TSessionContainer; Newer: TSessionContainer; LastAccess: TDateTime; public constructor Create(SessionClass: TSessionClass); destructor Destroy; override; end;
As we can see, the session container holds the session ID and a pointer to the session as well as the pointers needed in the list – Older and Newer. In addition to this, it holds the time that its session object was last accessed (for automatic eviction of sessions). We can also see that the constructor takes a session class type, not an actual session object. This is because the session container is responsible for the session object; when the session container is created, it automatically creates the session object of the correct type, and when it is destroyed, it automatically destroys the session object as well.
The time list is implemented by the TTimeList class, which exposes methods for adding a session, removing a session, and updating a session, which makes the specified session the “newest” one.
The hash table is implemented by the TSessionHashTable class, which implements methods for inserting a session container (associating it with a unique Cardinal ID), retrieving a session container given its ID, and removing a session container.
The main object, which uses the hash table and time list, and through which a user accesses the sessions, is the session manager, whose interface is shown below:
TSessionManager = class
protected
EvictionTimer: TTimer;
SessionClass: TSessionClass;
SessionTimeList: TTimeList;
SessionHashTable: TSessionHashTable;
EvictionTimeSeconds: Cardinal;
procedure EvictionTimerTimer(Sender: TObject);
function GenerateSessionID: Cardinal;
public
function NewSession: TSession;
function GetSession(aID: Cardinal): TSession;
function RemoveSession(aID: Cardinal): Boolean;
procedure Clear;
constructor Create(aSessionClass: TSessionClass;
aEvictionTimeSeconds: Cardinal = 600);
destructor Destroy; override;
end;
A user calls NewSession to retrieve a new session. NewSession creates a session and a session container, gives them a unique ID and adds them to the hash table and the time list.
To access an existing session, a user calls GetSession, which uses its hash table to quickly locate the correct session, and then calls the time list’s Update method to make that container the “newest” item in the time list.
To explicitly remove a session, a user calls RemoveSession, which internally locates the correct session using its hash table, and them removes it from both the hash table and the time list.
Sessions that have not been used for a while will be automatically removed and freed by the session manager’s eviction timer.
You can download the code here. There, you will find a unit test of the session classes as well as a visual test allowing you to create, access and remove sessions and watch how the contents of the hash table and the time list change. The session classes will be put to use in the next article, where I will show you how to create a simple socket-based web server.